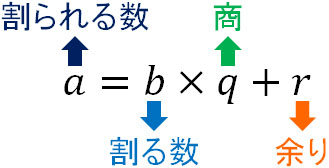
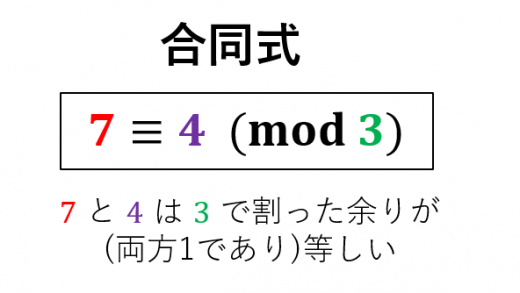
Web "割った余りが等しい"という記号 合同式の定義 M で割った余りを考える。 n と m を M で割った余りがそれぞれ等しいとき n ≡ m ( m o d M) と書く。 特に誤解の恐れが無い
数学 余り 記号-Web 数学は、等しくないものを同じ記号で表すことを嫌います。 だから \(Q(x)\)と\(Q(1)\)のように書き分けている のです。 ちなみに、一次式で割っているので、余り\(R\)はWeb複数の集合 A _ 1, A _ 2, \ldots, A _ n A1,,,An で和や積を取るときは以下の表記が用いられる。 \begin {aligned} \bigcup _ {i=1} ^ n A _ i &\stackrel {\mathrm {def}} {=} A _ 1 \cup A _ 2
数学 余り 記号のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  |  |
 | ||
「数学 余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「数学 余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「数学 余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 |  |  |
「数学 余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「数学 余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「数学 余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「数学 余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 |  | |
「数学 余り 記号」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |
Web代数記号 数学代数の記号と記号のリスト。 代数数学記号表 シンボル シンボル名 意味/定義 例;Web a mod n = bで 「bはaをnで割った時の余り(剰余)」 ということですよ。 例) 12 mod 7 = 5 16 mod 4 = 0 10 mod 3 = 1 ≡ (合同)という記号を使って、 a ≡ b (mod n) という
Incoming Term: 数学 余り 記号,




0 件のコメント:
コメントを投稿